Code Đại Chiến Tam Quốc mới nhất 2023 là gì? Code Đại Chiến Tam Quốc là một chuỗi mã được…
Bạn đang tìm hiểu về danh sách code chiến long tam quốc mới nhất năm 2023 và cách sử dụng…
Bạn muốn biết thêm về code chiến ký chư thần mới nhất?Điều tuyệt vời là code Chiến Ký Chư Thần…
Bạn muốn tìm hiểu về code Chiến Binh Vũ Trụ mobile mới nhất? Hãy khám phá mã Code Chiến Binh…
Bạn đang tìm kiếm danh sách Code Chiến Binh Truyền Thuyết mới nhất năm 2023? Trò chơi Chiến Binh Truyền…
Bạn đang chơi game Chiến Binh Tối Thượng và muốn có những code chiến binh tối thượng mới nhất để…
Bạn có muốn biết danh sách các mã code chaos battle trận chiến vĩnh hằng năm 2023 không? Chaos Battle…
Bạn có muốn biết danh sách code chân mệnh thiên tử mới nhất năm 2023 và cách nhập code? Trong…
Bạn đang tìm kiếm danh sách code chân mệnh tam quốc mới nhất năm 2023 và cách nhập code? Không…
Trong bài viết này, chúng ta sẽ tìm hiểu về mã code champion simulator mới nhất. Có rất nhiều mã…
Bạn có tò mò và muốn biết về những mã code champion battle mới nhất để tăng cường sức mạnh…
Bạn đã từng muốn khám phá code Call of Antia mới nhất và muốn biết cách nhập code Call of…
Bạn đã nghe về Code Cái thế tranh hùng mới nhất và muốn khám phá nó? Trò chơi này hứa…
Bạn muốn khám phá những mã code burger tycoon mới nhất và cách để nhập mã code trong trò chơi…
Bạn đã bao giờ muốn trở thành kiến trúc sư và xây dựng những tòa nhà vĩ đại của riêng…
Bạn muốn khám phá game Build a Boat for Treasure mới nhất và muốn biết cách nhập mã code trong…
Bạn muốn khám phá code bugtopia mới nhất và biết cách nhập code bugtopia? Bugtopia là một tổ chức chuyên…
Bạn đã từng khám phá vũ trụ của các chiến binh budo chưa? Hãy tiếp tục trải nghiệm với code…
Bạn đã từng thử chơi Bubble Gum Simulator và tìm hiểu về code bubble gum simulator mới nhất? Đây là…
Bạn đã từng nghe về code bubble gum mới nhất và muốn khám phá nó là gì? Hãy chuẩn bị…
Bạn đã bao giờ muốn tìm hiểu về bữa tiệc nhịp tim? Code bữa tiệc nhịp tim mới nhất sẽ…
Dưới đây là tổng hợp toàn bộ mã Code Boss Fighting Simulator mới nhất, được cập nhật liên tục. Hãy…
Hãy nhận ngay những mã Code Chakra Resonance mới nhất để giúp cho những game thủ có thể đổi những…
Bạn đang tìm kiếm những Code Chakra Fight Shinobi Belief mới nhất? Chakra Fight Shinobi Belief là một trò chơi…
Bạn đang tìm kiếm các Code Chainsaw Man Devil’s Heart mới nhất?Chainsaw Man Devil’s Heart kết hợp cốt truyện của…
Bạn muốn khám phá về mã Code CDO2 Dungeon Defense mới nhất? CDO2 Dungeon Defense là một trò chơi di…
Bạn muốn tìm hiểu về Code Car Factory Tycoon Mới Nhất? Car Factory Tycoon là một trò chơi trên Roblox,…
Bạn đang quan tâm đến các Code Car Dealership Tycoon mới nhất? Car Dealership Tycoon là một trò chơi nổi…
Bạn muốn biết về code Captor Clash mới nhất? Captor Clash là một trò chơi chiến đấu hấp dẫn với…
Bạn có đang chơi và muốn tìm mã code Cannon Simulator mới nhất? Bài viết này longky sẽ tổng hợp…
Hãy sử dụng các mã Code Call of Kings mới nhất dưới đây để đổi những phần thưởng có giá…
Với Code Call of Dragons mới nhất, bạn có thể nhận được một số phần thưởng đặc biệt khi mới…
Muốn khám phá code brown dust 2 mới nhất? Chắc chắn bạn sẽ bị mê hoặc bởi hệ thống Gacha…
Brick Bronze Odysseys là một trò chơi trên nền tảng Roblox, mang bạn vào thế giới của Brick Bronze. Bạn…
Code brave warriors combat Mới Nhất giúp bạn nhận được nhiều phần thưởng có giá trị như kim cương và…
Bạn đã nhận được code brave souls viscera espada Mới Nhất để sẵn sàng bắt đầu một hành trình huyền…
Bạn đang tìm kiếm mã code Brave Reapers Soul Maxima mới nhất? Bạn tìm đúng rồi đấy! Chúng tôi có…
Khi bạn tham gia Brain Simulator, bạn sẽ trở thành một nhà khoa học bằng cách thu thập nhiều bộ…
Ưu đãi hấp dẫn! Nhận ngay những mã code Bộ Xương Nhỏ mới nhất năm 2023 và khám phá cách…
Trong bài viết này, tôi sẽ hướng dẫn cho bạn cách nhập mã code box simulator Mới Nhất từ nhà…
Hãy cùng tìm hiểu mã code boxing friends simulator Mới Nhất và cách nhập chúng trong trò chơi boxing friends…
Phần mềm boxing beta năm 2023 đã ra mắt, và hãy cùng longky khám phá cách nhập code boxing beta…
Bạn là một người yêu thích sự hồi hộp và thách thức trong các trò chơi trên Roblox? Bạn muốn…
Bạn là người đam mê trải nghiệm các tựa game thú vị trên Roblox? Bạn đang tìm kiếm cơ hội…
Nếu bạn đang tìm kiếm cơ hội để tăng cường sức mạnh và trải nghiệm cuộc phiêu lưu đỉnh cao…
Chào các anh hùng trong thế giới Boku No Roblox Mastered! Bạn đang tìm cách nhanh chóng gia tăng tài…
Chào các thợ săn kho báu của Blox Fruit! Bạn đang tìm kiếm cách nhanh chóng tăng cường kinh nghiệm…
Bạn có hứng thú với việc nhận quà miễn phí trong game Bloody Treasure không? Nếu có, hãy tiếp tục…
Bạn đang tìm kiếm danh sách mã code Blood Route mới nhất cho người chơi mới năm 2023? Vậy thì…
Bạn có đang chơi trò chơi Bloodline Heroes of Lithas và muốn nhận được thêm lượng kim cương và vàng?…
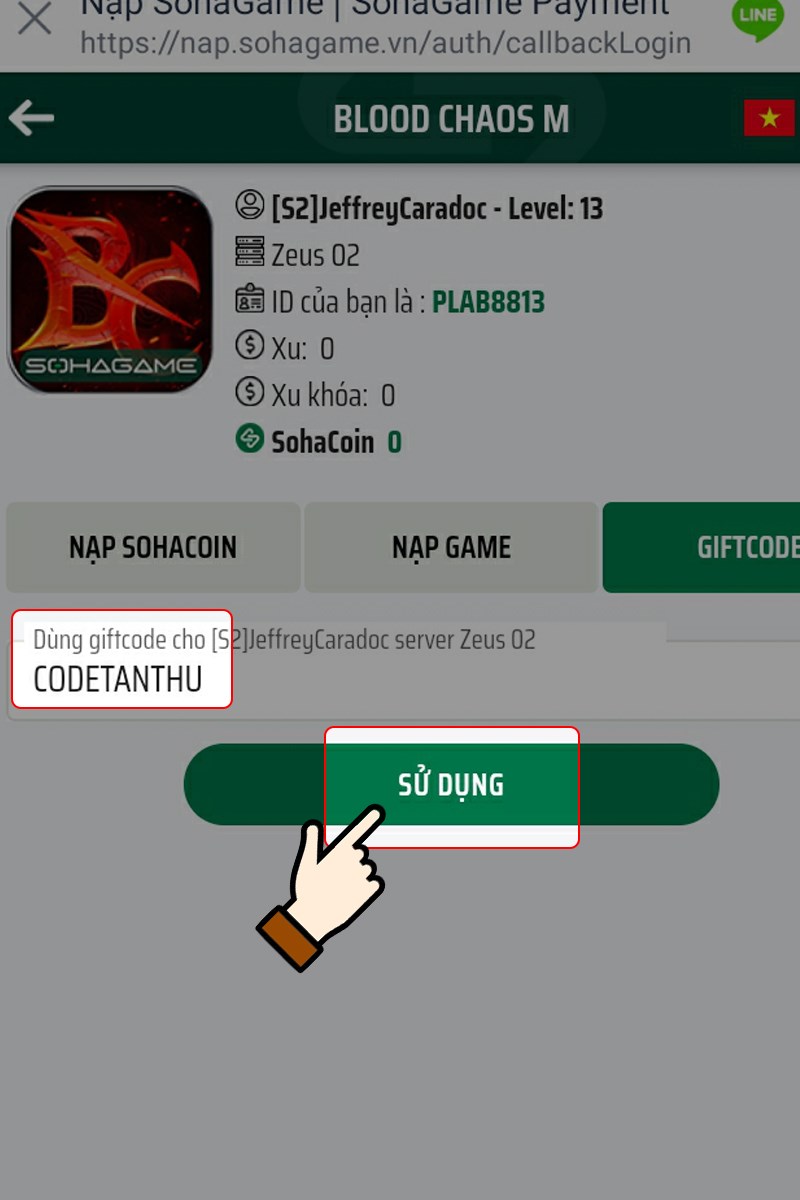
Bạn đang tìm hiểu về mã code Blood Chaos M mới nhất và cách sử dụng chúng? Trong bài viết…